十大排序算法 测试数据量：1000 0000（1千万） 数组 数据范围 100 0000（1百万）
以下是我在自己的笔记本上的运行时间统计：
（1）冒泡排序  排序用时：105626毫秒~  (20万)    复杂度高 不选择
（2）选择排序  排序用时：56199毫秒~  (20万)    复杂度高 不选择
（3）插入排序  排序用时：6060毫秒~  (20万)    适用于数据量小 且已接近有序的数据集
（4）希尔排序  排序用时：4144毫秒~   (1000万)  插入排序的改进 适用于大量数据集
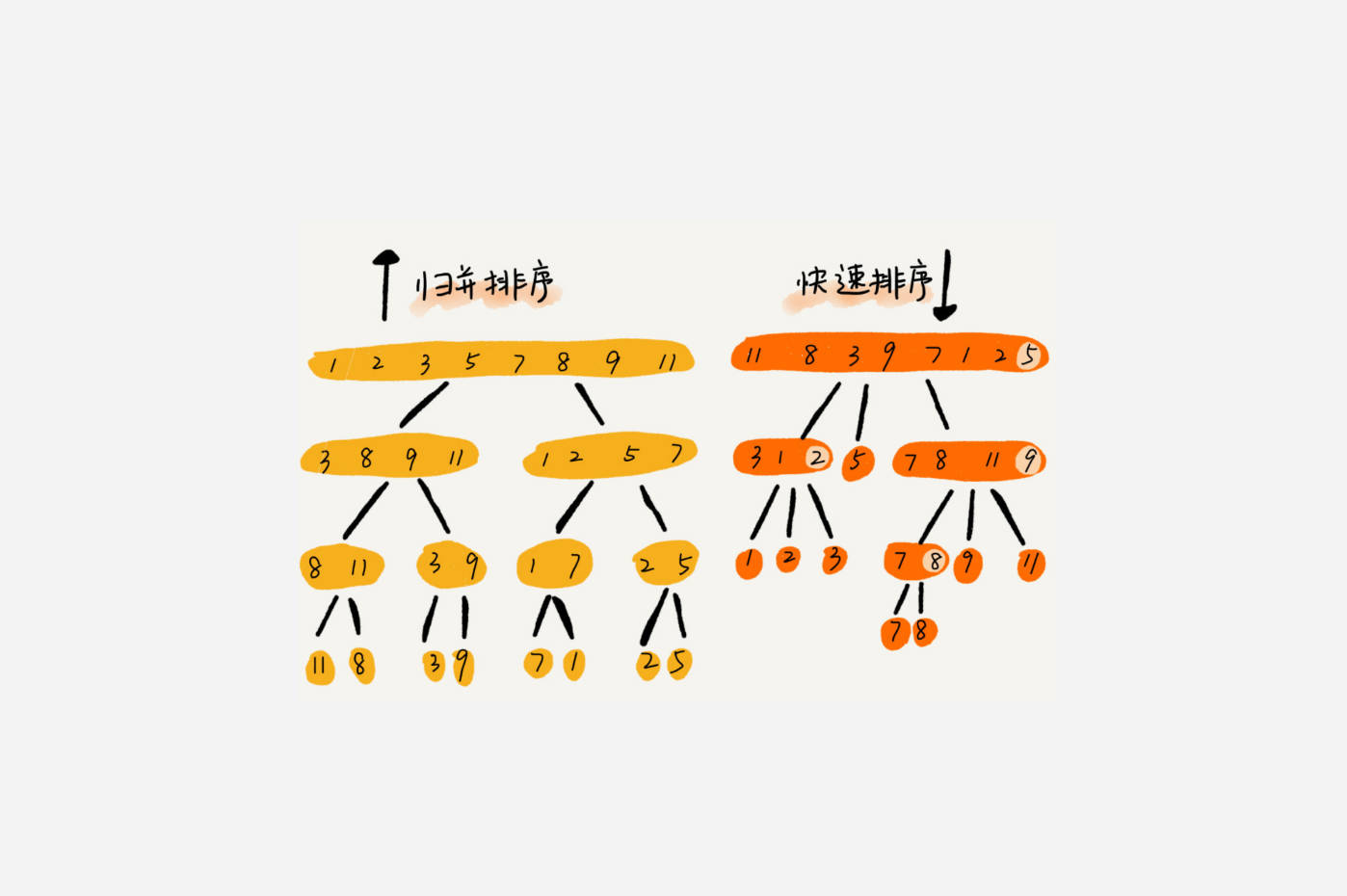
（5）归并排序  排序用时：3862毫秒~   (1000万)  适用于大量数据集 但相对于快速排序会多占用内存空间
（6）堆排序    排序用时：3824毫秒~   (1000万)  可用于对大量数据集的排序 但性能不如快速排序
（7）快速排序  排序用时：2033毫秒~   (1000万)  综合性能优秀 但当数据集数据量大且基本有序的时候复杂度会降低到O(n2)
（8）计数排序  排序用时：132毫~      (1000万)  适用于数据量小且分布范围较小 分布密秒度高的数据集
（9）桶排序    排序用时：6272毫秒~ 100桶 (1000万)
             排序用时：4232毫秒~ 10000桶  (1000万)
  适用于数据集分布均匀的数据集 为何说桶排序的时间复杂度可以趋近O(n)?
  因为当桶的数量足够多 每个桶的数据量就会非常小 对其进行插入排序所用的时间也趋于常数级别
（10）基数排序 适用于需要对数据的不同模块按照不同的优先级进行排序的场景 例如 依次按照学生的语文 数学 英语成绩进行排序

private static void quickSort(int[] a, int l, int r) { 
    // 子数组当中只有一个元素的时候 会直接返回
    if (l >= r) return; // [l, r]

    // 获取基准点（这个分区函数在后面实现）
    int p = partition(a, l, r); 
    // 递归对基准数左右两侧的子数组进行快排
    quickSort(a, l, p - 1);
    quickSort(a, p + 1, r);
}

public static int partition(Integer[] a, int l, int r) {
    // 选取基准元素base
    int base = a[l]; 
    // ij主键靠近 完成元素以base为中间元素 分布在左右两边
    int i = l, j = r;

    // 要求从小到大排序
    while(i < j) {
        // j从右到左寻找一个比base小的数
        while(i < j && a[j] >= base) --j;
        // 找到后与i所在的位置进行替换
        if(i < j) { a[i] = a[j]; ++i; }

        // i从左到右寻找一个比base大的数
        while(i < j && a[i] <= base) ++i;
        // 找到后与j所在的位置进行替换
        if(i < j) { a[j] = a[i]; --j; }
    }

    // while循环结束 这时ij指向同一个位置 把base赋值给a[i/j]
    a[i] = base;
    // 返回中间元素下标
    return i;
}

/**
 * 堆排序
 * @param a        要排序的数组
 * @param minOrMAX 最大堆还是最小堆 0 最小堆 1 最大堆
 */
private static void heapSort(int[] a, int minOrMAX) {
    // 首先还是建堆 从最后一个为叶子结点执行堆调整函数 
    // 直到整个堆呈最大堆或最小堆的形式
    for(int i = a.length >>> 1 - 1; i >= 0; --i) {
        adjustHeap(a, i, a.length, minOrMAX);
    }

    // 执行排序
    int size = a.length;
    while(size > 0) {
        // 每次从堆顶元素取数 放置到数组末尾 这样就完成了一个数的排序
        int t = a[0]; a[0] = a[--size]; a[size] = t;
        // 调整堆以确定下一个堆顶元素
        adjustHeap(a, 0, size, minOrMAX);
        // 直到所有的数完成排序 函数结束
    }
}

/**
 * 堆调整
 * @param a         要调整的堆
 * @param p         当前调整的元素的下标 parent
 * @param size      数组当前逻辑上的大小
 * @param minOrMAX  标识是大根堆还是小根堆
 */
private static void adjustHeap(int[] a, int p, int size, int minOrMAX) {
    int l = p * 2 + 1; // 获取当前结点的左孩子下标
    int r = p * 2 + 2; // 获取当前结点的右孩子下标
    int m = p;         // 指向父节点和左右孩子节点中最大值的下标

    // 根据堆是否是大根堆还是小根堆进行动态处理 更新m下标
    if(l < size && (minOrMAX == MIN ? a[l] < a[m] : a[l] > a[m])) m = l;
    if(r < size && (minOrMAX == MIN ? a[r] < a[m] : a[r] > a[m])) m = r;

    // 如果m被更新 说明找到了比父节点更大或更小的数
    if(m != p) {
        // 执行交换调整
        int t = a[m]; a[m] = a[p]; a[p] = t;
        // 继续调整 直到m下标没有孩子节点 或者m指向的元素满足堆顶特性（最大或最小）
        adjustHeap(a, m, size, minOrMAX);
    }
 }