计算机基础数据结构与算法递归&回溯

🎄概述

🍭递归

递归是一种自我调用的算法技巧。在递归中，一个问题可以通过调用自身来解决。递归算法包括基本情况和递归情况。基本情况是递归的终止条件，当满足该条件时，递归停止并返回结果。递归情况是指将问题分解为更小的子问题，并通过递归调用解决这些子问题。通常，递归算法需要构建一个递归函数或方法，并确保每次调用都朝着基本情况推进，否则可能导致无限循环。

递归求解出所有的可能性假设其结果集是A

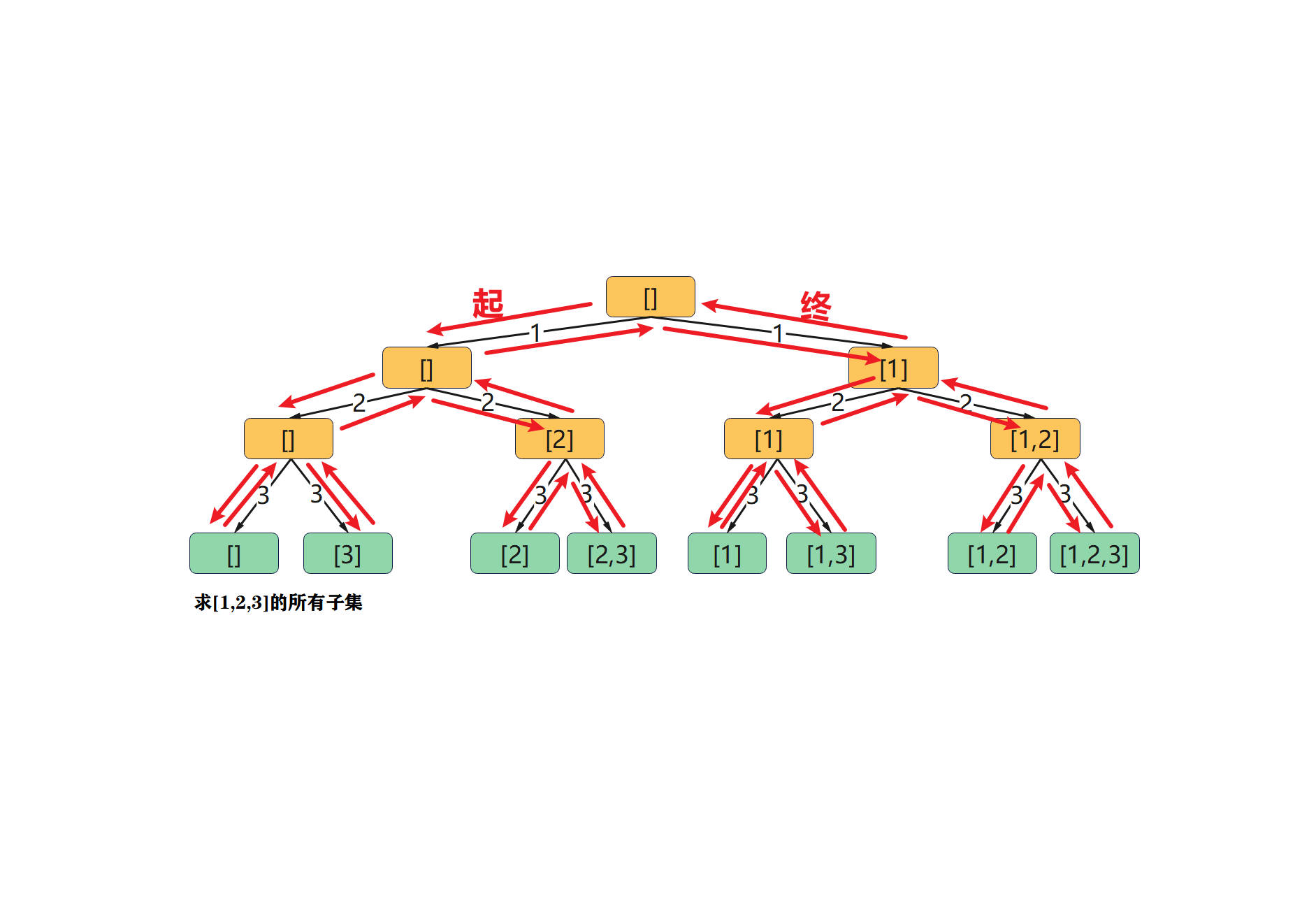
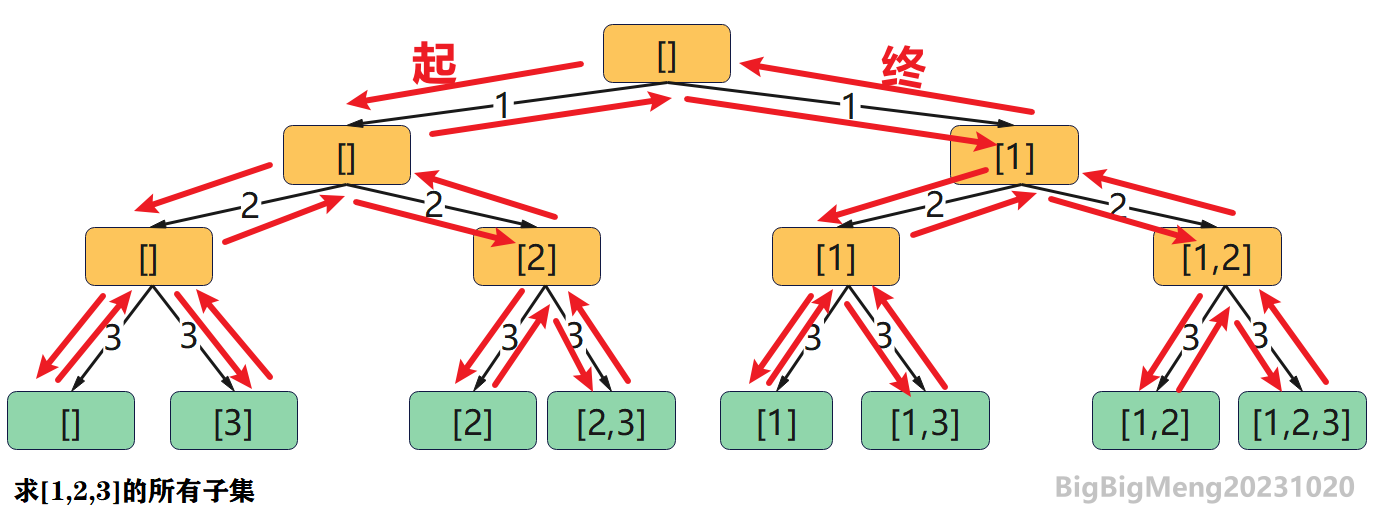
【举例】给出一个不重合的数字n 求出这些数字（1~n）所有的子集假设给出的n=3 就相当于求{1,2,3}的所有子集则用递归可以求解出下面的结果：

所有的蓝色数组序列的集和是最终的结果集A = {[],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3]}

🍭回溯

回溯是一种通过尝试不同的选择来寻找问题解的算法技术。回溯算法通常用于解决组合优化问题，如排列、组合、子集等。回溯算法通过构建一个决策树或状态空间树，不断尝试每个可能的选择，并在发现不能得到有效解的情况下回溯到上一级选择进行另一种尝试。回溯算法通常使用递归来实现，每次递归调用对应于一个选择，递归返回回到上一级选择。

回溯算法是在递归的基础上加入了特定的搜索和剪枝策略，以便高效地搜索问题的解空间经过剪枝（条件判断）从而不去执行某些递归分支相当于在递归中删除了一些结果假设其结果集是B 则A包含B

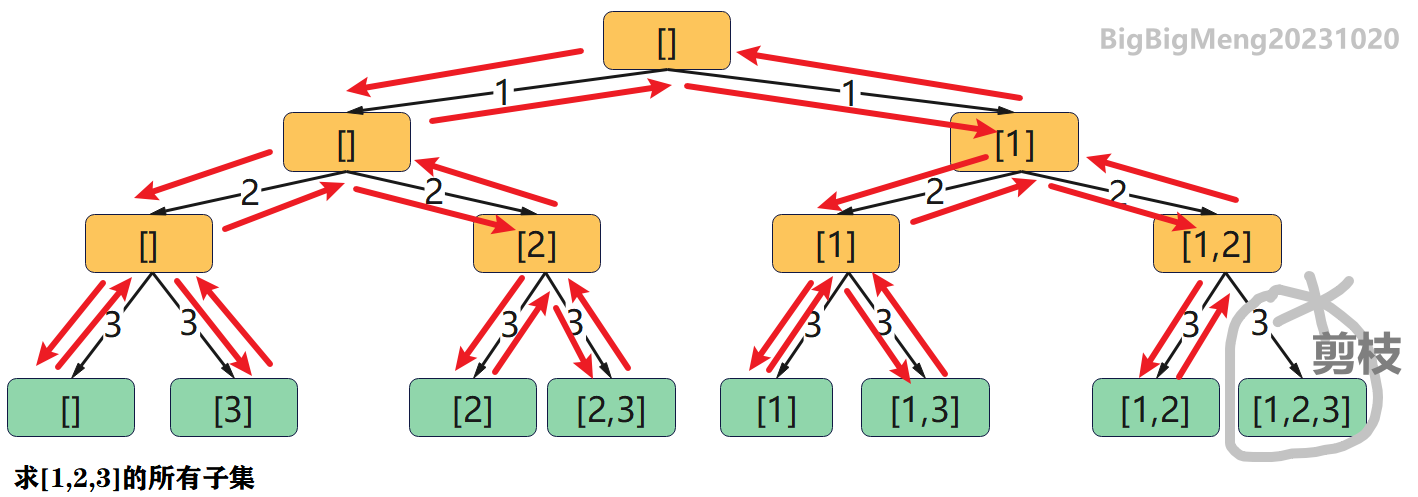
【举例】同样使用上面的示例在其基础上追加一个条件：子集大小度最大元素个数为2 这个时候递归调用和原来一样只不过加了一些条件限制：

在程序执行的过程中当序列的长度已经等于2了则直接返回不再往深继续递归这就是剪枝不再去生成长度为3的序列结果所有的蓝色数组序列的集和是最终的结果集B = {[],[1],[2],[3],[1,2],[1,3],[2,3]}

🍭递归和回溯

递归和回溯经常同时出现在问题解决过程中。在一些情况下，递归可以用于生成所有可能的解空间（如组合、排列等），而回溯用于剪枝和寻找有效解。递归和回溯都是非常强大的算法工具，可以解决很多复杂的问题。然而，由于递归的性质，其时间复杂度可能会很高，并且需要合理设计递归终止条件和剪枝策略，以减少无效的计算和提高算法效率。

🎄题目实战

⚡所有子集

📑题目描述

输入一个不包含重复元素数字的数据集合请找出它的所有子集例如：数据集合[1,2]有4个子集分别是 []、[1]、[2]、[1,2]

方法1 剑指offer

代码来自剑指offer 注释来自🌱BigBigMeng

🎯算法分析

/**
@author Liu Xianmeng
@createTime 2023/10/19 20:25
@instruction
*/
public class Test {
    /**
     * 完成最终结果的生成
     * @param a     传入的原数组
     * @return
     */
    public List<List<Integer>> subsets(int[] a) {
        List<List<Integer>> rst = new LinkedList<>();
        // 数组长度的判断 如果数组为空 则是直接返回空结果
        if(a.length == 0) return rst;

        // 执行辅助函数 完成子集的生成和填充
        helper(a, 0, new LinkedList<Integer>(), rst);
        // 返回结果
        return rst;
    }

    /**
     * 辅助函数 -> 递归调用
     *
     * 函数的内部分两种情况
     * (1) i = a.length -> a数组所有的元素都已经遍历完了 直接把子集subset放入rst 然后return
     * (2) i < a.length -> a数组的元素还没有遍历完 这个时候又要分两种情况
     *     (2.1) 把当前的i下标对应的元素加入子集subset 然后去处理 i + 1 下标对应的元素 -> ⚡这个地方产生递归
     *     (2.2) 忽略当前i下标对应的元素 直接去处理 i + 1 下标对应的元素 -> ⚡这个地方产生递归
     *
     * @param a         原数组
     * @param i         原数组中当前遍历到的元素的下标
     * @param subset    调用helper函数时已经生成的子集
     * @param rst       最终生成的结果
     */
    private void helper(int[] a, int i, LinkedList<Integer> subset, List<List<Integer>> rst) {
        /**** (1) i = a.length -> a数组所有的元素都已经遍历完了 直接把子集subset放入rst 然后return ****/
        if(i == a.length) {
            rst.add(new LinkedList<>(subset));
            return;
        }

        /**** (2) i < a.length -> a数组的元素还没有遍历完 这个时候又要分两种情况 ****/
        // (2.1) 把当前的i下标对应的元素加入子集subset 然后去处理 i + 1 下标对应的元素 -> 这个地方产生递归
        subset.addLast(a[i]);
        helper(a, i + 1, subset, rst);
        subset.removeLast(); // 在处理(2.2)之前 要把加入的a[i]元素删除 使得(2.1)和(2.2)处理的subset是一样的

        // (2.2) 忽略当前i下标对应的元素 直接去处理 i + 1 下标对应的元素 -> 这个地方产生递归
        helper(a, i + 1, subset, rst);
    }
}

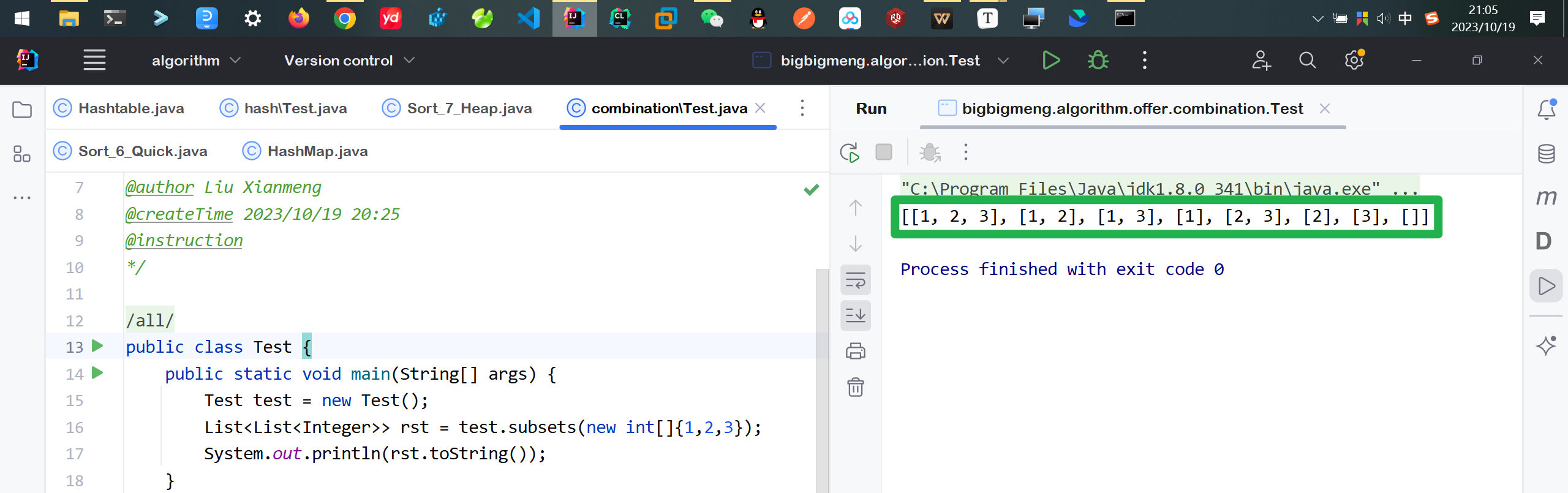
🎯执行测试

public static void main(String[] args) {
    Test test = new Test();
    List<List<Integer>> rst = test.subsets(new int[]{1,2,3});
    System.out.println(rst.toString());
}

方法2 🌱BigBigMeng

我在看《剑指offer》这本书的时候发现读起来有点费力因为作者每次会直接把完整的代码直接附在题目的描述后先把代码整个全部放上来再在后面进行整段的解释我认为重要的注释放在代码里会更好读解释的时候要不停地回看源码…

为什么会有方法2 ? 作者直接把 private void helper(int[] a, int i, LinkedList<Integer> subset, List<List<Integer>> rst){..} 却没有解释为什么要这样设置这个函数的参数为什么这个函数的参数要有int[] a ? 不要这个参数行不行？作者也没有说

如果只是记住了题解的答案那么之后大概率很快就会忘记而明白解题思路才是王道

所以helper为什么要传入4个参数？我传入3个行不行？看下面的算法分析

🎯算法分析

/**
 * 见名知意 handleNextInteger -> 处理下一个整数
 * 
 * ❌不能这么设计这个函数
 * @param num       此时要处理的原数组的元素
 * @param subset
 * @param rst
 */
private void handleNextInteger(int num, LinkedList<Integer> subset, List<List<Integer>> rst) {
    // 如果这么设计 似乎有点问题
    // ❌如何在函数内部确定下一个数字？如果这么设计这个函数，那么在递归调用的时候就无法确定下一个数了 哈哈哈 所以说还是得传入原数组和下标才行... 作者是对的🙃 再进行思考 就明白了递归调用的函数里面必须含有递归函数里面要用到的参数才行
}

其实这是我的思考的总结所以方法2 没能出生💩

再来看作者对helper函数的设计理解就会更加深刻

private void helper(int[] a, int i, LinkedList<Integer> subset, List<List<Integer>> rst){
    // 在函数的内部 需要根据数组a 和下标i 去确定当前要处理的元素
    // 在递归调用中 只需要对i做变化即可
    
    // 其实subset和rst的设计也是巧妙的 因为他们都是引用类型 所以在整个调用过程中做的修改都算数
    // 在后面的递归调用中都起作用 是动态变化的 
    if(i == a.length) {
        // 所以在退出的时候rst.add(new LinkedList<>(subset)) 而不是rst.add(subset)
        rst.add(new LinkedList<>(subset));
        return;
    }
    ...
}

下次再遇到此类题目就能回想自己的思路来解决而不是单纯地记住题解记题解没有任何意义没搞明白那就浪费时间了

⚡包含k个元素的组合

📑题目描述 输入n和k 请从1到n中选取k个数字组成的所有组合例如：如果n=3 k=2 则结果集 = [[1,2],[1,3],[2,3]]

🎯题目分析

其实这个题和第一题几乎没有区别（1）既然是选取k个数字那么就说明每个数字都不一样（2）指定选取k个数则组合中只有k个数相当于从所有结果中筛选出元素数目为k的组合形成最终的结果集

🎯算法分析

package bigbigmeng.algorithm.offer.combination;

import java.util.LinkedList;
import java.util.List;

/**
@author Liu Xianmeng
@createTime 2023/10/19 20:25
@instruction
*/

@SuppressWarnings({"all"})
public class Test {
    public static void main(String[] args) {
        Test test = new Test();
        LinkedList<LinkedList<Integer>> rst = test.getCombinations(5, 4);
        System.out.println(rst.toString());
        /** OutPut
         * [[2, 3, 4, 5], [1, 3, 4, 5], [1, 2, 4, 5], [1, 2, 3, 5], [1, 2, 3, 4]]
         */
    }

    /**
     * 通过调用handle函数使得经过一系列的处理后获取到组合集
     * @param n     [1,n]
     * @param k     组合的树个数为k
     * @return
     */
    private LinkedList<LinkedList<Integer>> getCombinations(int n, int k) {
        // 存储结果
        LinkedList<LinkedList<Integer>> rst = new LinkedList<>();
        // 一个新的组合
        LinkedList<Integer> combination = new LinkedList<>();
        // 递归处理过程 n用作终止条件的判断 所以必须有这个参数
        handle(n, k, 1, combination, rst);
        // 返回结果
        return rst;
    }

    /**
     * 处理过程
     * 
     * @param n             用作退出条件的判断
     * @param k
     * @param i             遍历到的数
     * @param combination   中间过程集合
     * @param rst
     */
    private void handle(int n, int k, int i, LinkedList<Integer> combination, LinkedList<LinkedList<Integer>> rst) {
        // 终止条件
        if(combination.size() == k){
            rst.add(new LinkedList<>(combination));
        } else if(i <= n){
            // 1 不处理当前元素
            handle(n, k, i + 1, combination, rst);
            
            // 2 处理当前元素
            combination.addLast(i);
            handle(n, k, i + 1, combination, rst);
            combination.removeLast();
        }
    }
}

⚡允许重复选择元素的组合

📑题目描述 给定一个没有重复数字的正整数集合，请找出所有元素之和等于某个给定值sum的所有组合。同一个数字可以在组合中出现任意次。例如，输入整数集合[2，3，5]，元素之和等于8的组合有3个，分别是[2，2，2，2]、[2，3，3]和[3，5]。

🎯题目分析

这个题目和 包含k个元素的组合 有什么区别呢？（1）递归终止条件不一样，这个题的终止条件是组合的元素的和恰好等于所给的sum 这个时候就生成一个符合条件的组合（2）元素可以重复使用

🎯算法分析

package bigbigmeng.algorithm.offer.combination;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

/**
@author Liu Xianmeng
@createTime 2023/10/19 20:25
@instruction
*/

@SuppressWarnings({"all"})
public class Test {
    public static void main(String[] args) {
        System.out.println(getCombinations(new int[]{2,3,5}, 8).toString());
        /**OutPut
         * [[3, 5], [2, 3, 3], [2, 2, 2, 2]]
         */
    }

    /**
     * 获取最终的结果 rst
     *
     * @param a
     * @param sum       要求组合中数的和 === sum
     * @return
     */
    public static LinkedList<LinkedList<Integer>> getCombinations(int[] a, int sum) {
        // 从小打大排序后再处理
        Arrays.sort(a);
        // 存储结果
        LinkedList<LinkedList<Integer>> rst = new LinkedList<>();
        // 一个空的组合
        LinkedList<Integer> combination = new LinkedList<>();
        // 处理 -> 获取最终的结果并存储在rst中
        handle(a, 0, sum, combination, rst);
        // 返回结果
        return rst;
    }

    /**
     * 处理 -> 获取最终的结果并存储在rst中
     *
     * @param a             原数组
     * @param i             数组下标 -> 用于获取数组的元素
     * @param remainSum     剩下的和（生成的组合的所有数和加和===sum）
     * @param combination
     * @param rst
     */
    private static void handle(int[] a, int i, int remainSum, LinkedList<Integer> combination, LinkedList<LinkedList<Integer>> rst) {
        // 终止条件 1
        if(i == a.length) return;

        // 终止条件 2 如果剩余的sum < 0 则说明不符合条件 进行回溯 直接返回
        if(remainSum - a[i] < 0) {
            return;
        }

        // 终止条件 3 如果剩余的sum == 0 则说明正好生成一个符合条件的结果
        if(remainSum - a[i] == 0) {
            combination.addLast(a[i]);
            rst.addLast(new LinkedList<>(combination));
            combination.removeLast();
            return;
        }

        /************** 其他情况继续递归 **************/

        // 1 不处理当前元素
        handle(a, i + 1, remainSum, combination, rst);

        // 2 处理当前元素
        combination.addLast(a[i]);
        // 注意这里传入的是⚡i而不是i+1 因为元素允许重复 所以添加了a[i]下一次还要判断a[i] 直到remainSum <= 0 递归终止
        handle(a, i, remainSum - a[i], combination, rst);
        combination.removeLast();
    }
}

仔细观察会发现上面的代码存在重复的问题 combination.addLast(a[i]) 和 combination.removeLast() 写了两遍因此不够优雅那如何修改handle函数呢看下面的代码

/**
 * 处理 -> 获取最终的结果并存储在rst中
 *
 * 只处理 remainSum == 0 和 remainSum > 0 的情况
 */
private static void handle(int[] a, int i, int remainSum, LinkedList<Integer> combination, LinkedList<LinkedList<Integer>> rst) {
    // 终止条件
    if(remainSum == 0) {
        // 生成结果
        rst.add(new LinkedList<>(combination));
    } else if(i < a.length && remainSum > 0) { // 注意终止条件 i < a.length
        // 继续递归

        // 1 不处理当前的 a[i]
        handle(a, i + 1, remainSum, combination, rst);

        // 2 处理当前的 a[i]
        combination.addLast(a[i]);
        handle(a, i, remainSum - a[i], combination, rst);
        combination.removeLast();
    }
}

运行结果：

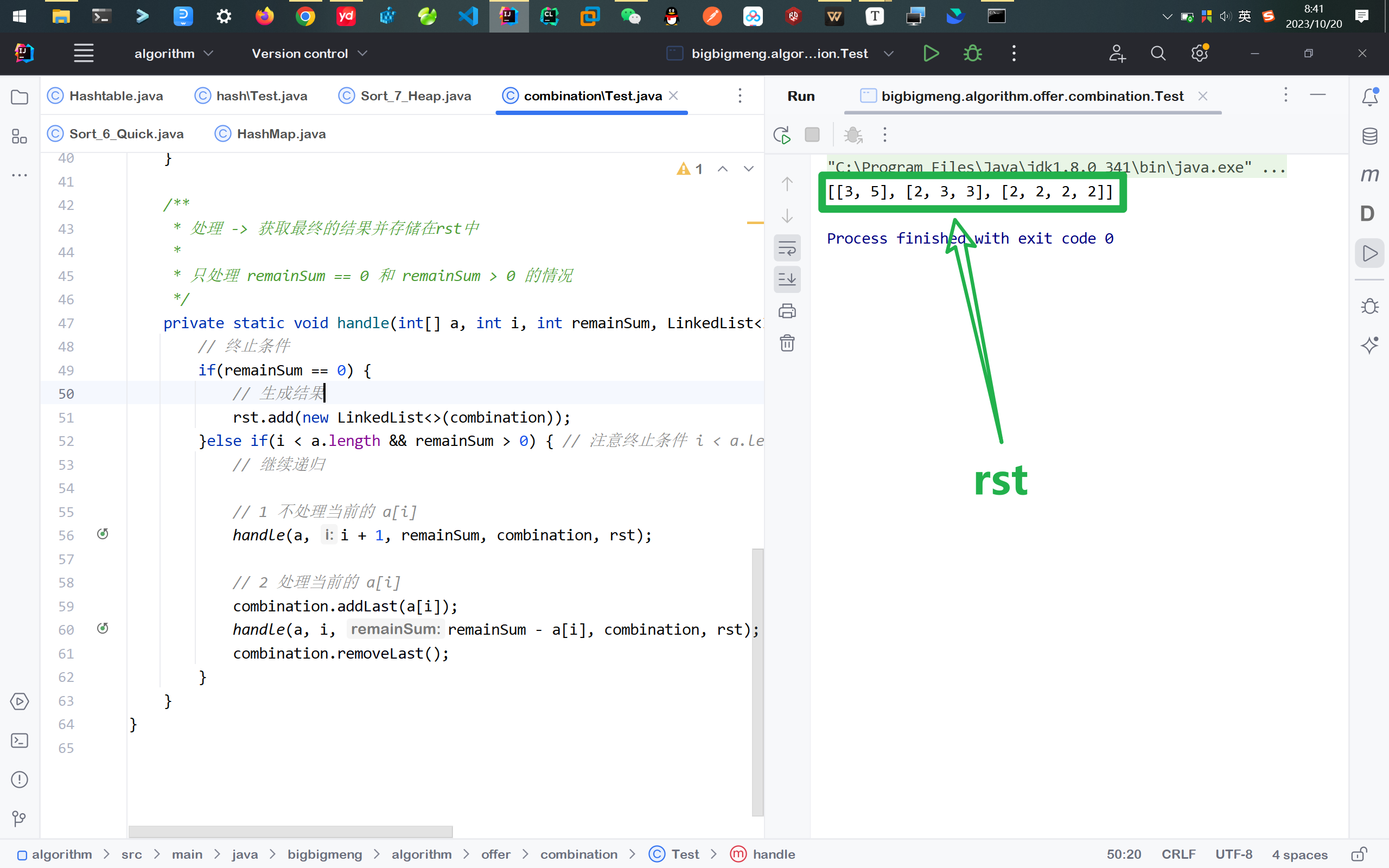
⚡思考1 不允许元素重复

❓如果不允许元素重复且和为sum 怎么改代码？

只需要把下面代码的🎯i改为i+1即可

// 2 处理当前的 a[i]
combination.addLast(a[i]);
handle(a, 🎯i, remainSum - a[i], combination, rst);
combination.removeLast();

这样最终的结果就只有 [3,5] 了

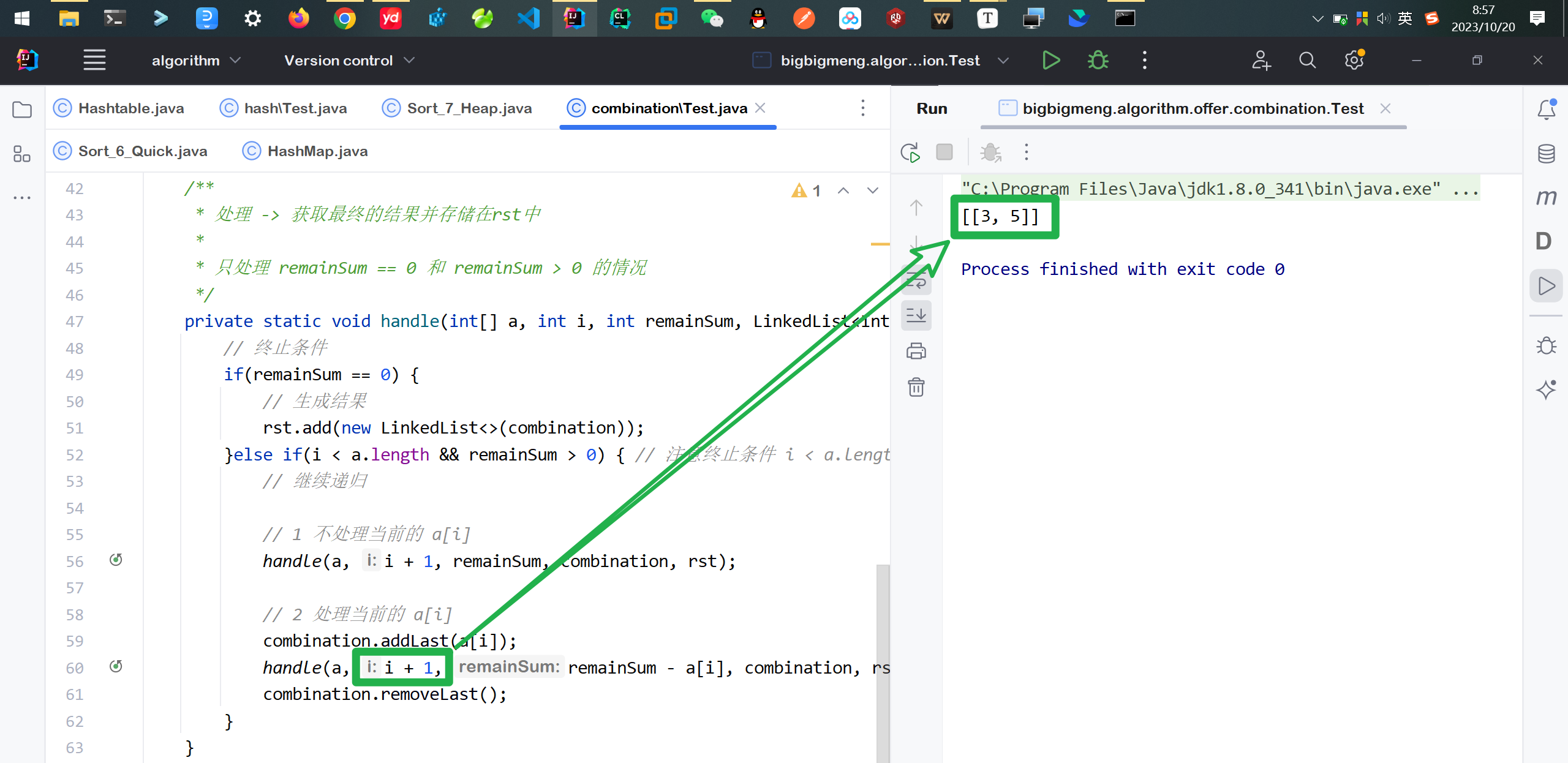
⚡思考2 只收集组合中只有4个数的结果

❓如果只想要4个数的组合且和为sum且允许元素重复怎么改代码？

只需要在终止条件加上combination.size() == 4的限制即可

// 终止条件
if(remainSum == 0 && 🎯combination.size() == 4) {
    // 生成结果
    rst.add(new LinkedList<>(combination));
}

这样最终的结果就只有 [2, 2, 2, 2] 了

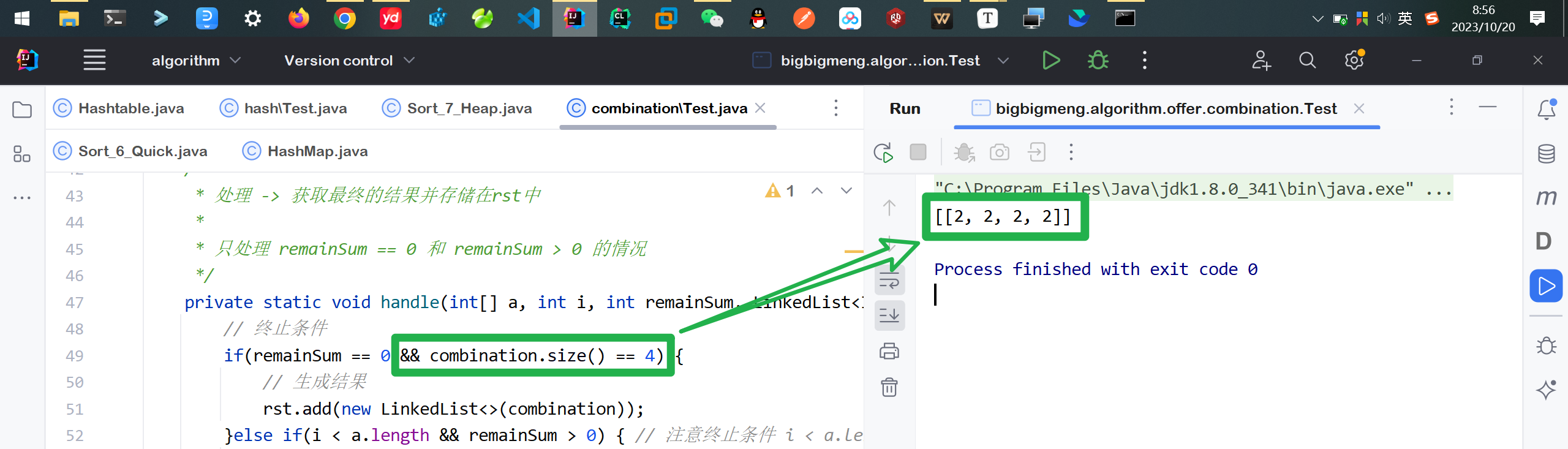
⚡包含重复元素集合的组合

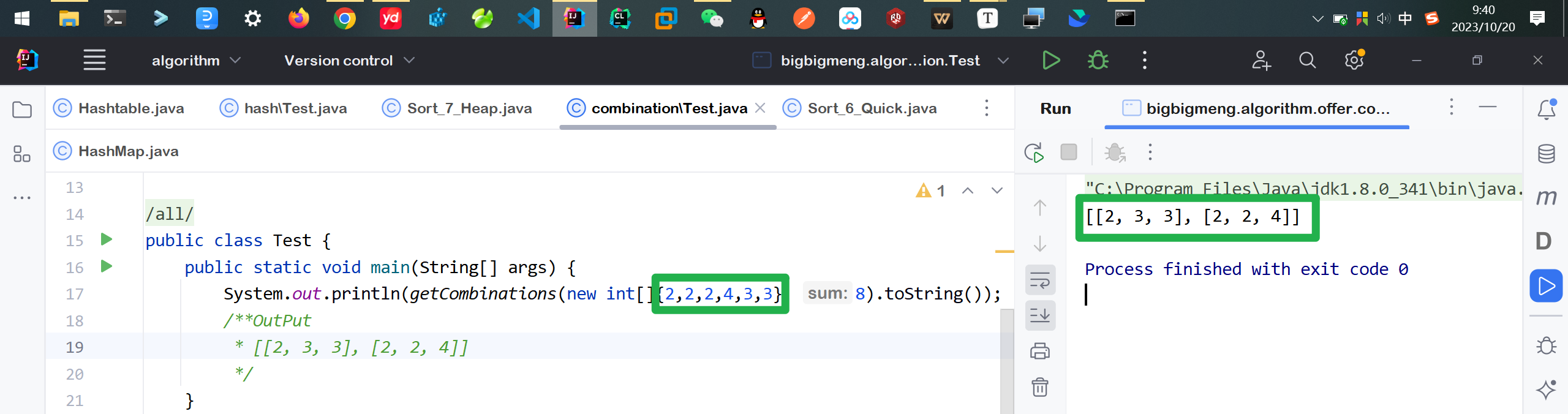
📑题目描述 给定一个可能包含重复数字的整数集合，请找出所有元素之和等于某个给定值的所有组合。输出中不得包含重复的组合。例如，输入整数集合[2，2，2，4，3，3]，元素之和等于8的组合有2个，分别是[2，2，4]和[2，3，3]。

🎯题目分析 && 算法分析

排序后再处理用一个map标记已经存在的结果组合

package bigbigmeng.algorithm.offer.combination;

/**
@author Liu Xianmeng
@createTime 2023/10/19 20:25
@instruction
*/
public class Test {
    public static void main(String[] args) {
        System.out.println(getCombinations(new int[]{2,2,2,4,3,3}, 8).toString());
        /**OutPut
         * [[2, 3, 3], [2, 2, 4]]
         */
    }

    /**
     * 获取最终的结果 rst
     *
     * @param a
     * @param sum       要求组合中数的和 === sum
     * @return
     */
    public static LinkedList<LinkedList<Integer>> getCombinations(int[] a, int sum) {
        // 从小打大排序后再处理
        Arrays.sort(a);
        // 存储结果
        LinkedList<LinkedList<Integer>> rst = new LinkedList<>();
        // 一个空的组合
        LinkedList<Integer> combination = new LinkedList<>();
        // HashMap存储标记 -> 标记已经存在的组合结果
        HashMap<String, String> map = new HashMap<>();
        // 处理 -> 获取最终的结果并存储在rst中
        handle(a, 0, sum, combination, rst, map);
        // 返回结果
        return rst;
    }

    /**
     * @param map           标记已经存在的结果组合
     */
    private static void handle(int[] a, int i, int remainSum, LinkedList<Integer> combination,
                               LinkedList<LinkedList<Integer>> rst, HashMap<String, String> map) {
        // 只收集之前没有出现的组合
        if(remainSum == 0 && map.get(combination.toString()) == null) {
            rst.add(new LinkedList<>(combination));
            // 每添加一个组合结果 就将其放入map
            map.put(combination.toString(), "");
            
        } else if(remainSum > 0 && i < a.length) {
            handle(a, i + 1, remainSum, combination, rst, map);

            combination.addLast(a[i]);
            handle(a, i + 1, remainSum - a[i], combination, rst, map);
            combination.removeLast();
        }
    }
}

⚡没有重复元素集合的全排列

📑题目描述 给定一个没有重复数字的集合，请找出它的所有全排列。例如，集合[1，2，3]有6个全排列，分别是[1，2，3]、[1，3，2]、[2，1，3]、[2，3，1]、[3，1，2]和[3，2，1]

🎯题目分析 && 算法分析

package bigbigmeng.algorithm.offer.combination;

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;

/**
@author Liu Xianmeng
@createTime 2023/10/19 20:25
@instruction
*/

@SuppressWarnings({"all"})
public class Test {
    public static void main(String[] args) { // 2,90,2,4,3,3
        System.out.println(getCombinations(new int[]{2,90,8}).toString());
        /**OutPut
         * [[8, 90, 2], [90, 8, 2], [90, 2, 8], [8, 2, 90], [2, 8, 90], [2, 90, 8]]
         */
    }

    /**
     * 获取最终的结果 rst
     *
     * @param a
     * @param sum       要求组合中数的和 === sum
     * @return
     */
    public static LinkedList<LinkedList<Integer>> getCombinations(int[] a) {
        // 存储结果
        LinkedList<LinkedList<Integer>> rst = new LinkedList<>();
        LinkedList list = new LinkedList<>();
        list.add(a[0]);
        rst.add(list);

        // 处理 -> 获取最终的结果并存储在rst中
        for(int i = 1; i < a.length; ++i) {
            // 暂存新的rst
            LinkedList<LinkedList<Integer>> tempRst = new LinkedList<>();
            // 遍历rst中的LinkedList
            for(int j = 0; j < rst.size(); ++j) {
                LinkedList<Integer> curList = rst.get(j);
                // 对curList中的每一个位置执行插入 生成新的组合 所有新的组合就是一个新的rst
                // rst会被更新 a.length - 1 次
                for(int k = 0; k <= curList.size(); ++k) {
                    curList.add(k, a[i]);
                    tempRst.add(new LinkedList<>(curList));
                    curList.remove(k);
                }
            }
            // 更新结果
            rst = tempRst;
        }
        // 返回结果
        return rst;
    }
}

🎄使用回溯法解决其他类型的问题

🌱思路总结

如果解决一个问题需要若干步骤，并且每一步都面临若干选项，当在某一步做了某个选择之后前往下一步仍然面临若干选项，那么可以考虑尝试用回溯法解决。通常，回溯法可以用递归的代码实现。

适用回溯法的问题的一个特征是问题可能有很多个解，并且题目要求列出所有的解。如果题目只是要求计算解的数目，或者只需要求一个最优解（通常是最大值或最小值），那么可能需要运用动态规划。

⚡生成匹配的括号

📑题目描述 题目：输入一个正整数n，请输出所有包含n个左括号和n个右括号的组合，要求每个组合的左括号和右括号匹配。例如，当n等于2时，有两个符合条件的括号组合，分别是"（()）“和”()()"

题目分析

求出一个符合条件的括号组合需要多个步骤具体是多少步呢？2*n步因为要求输出所有包含n个左括号和n个右括号的组合所以组合中包含2n个括号字符

什么情况下遇到的括号组合符合条件呢？当栈（用栈存储左括号）为空且已经遍历到第2n + 1个括号的时候

算法分析

package bigbigmeng.algorithm.offer.combination;
/**
@author Liu Xianmeng
@createTime 2023/10/19 20:25
@instruction
*/
public class Test {
    public static void main(String[] args) { // 2,90,2,4,3,3
        System.out.println(getCombinations(3).toString());
        /**OutPut
         * [((())), (()()), (())(), ()(()), ()()()]
         */
    }

    /**
     * 用n对括号组成的合法括号序列
     * @param n
     * @return
     */
    private static Object getCombinations(int n) {
        // 存储最终的结果
        LinkedList<String> rst = new LinkedList<>();
        // 存储已经出现的左括号
        LinkedList<Character> stack = new LinkedList<>();
        // 执行处理 收集结果到rst中
        handle(n, n, "", rst);
        // 返回结果
        return rst;
    }

    /**
     * 处理函数
     * @param left      左括号还剩下的个数
     * @param right     右括号还剩下的个数
     * @param sb        中间生成字符串
     * @param rst       结果集
     */
    private static void handle(int left, int right, String str, LinkedList<String> rst) {
        if(left == 0 && right == 0) {
            rst.add(str);
            return;
        }
        // 在递归过程中 只要left > 0满足则继续向下递归 拼接左括号
        if(left > 0) {
            handle(left - 1, right, str + "(", rst);
        }
        // 在递归过程中 只要right > left满足则继续向下递归 拼接右括号
        if(right > left) {
            handle(left, right - 1, str  + ")", rst);
        }
    }
}

递归展开过程

/**
 * 处理函数
 * @param left      左括号还剩下的个数
 * @param right     右括号还剩下的个数
 * @param sb        中间生成字符串
 * @param rst       结果集
 */
private static void handle(int 2, int 2, String str, LinkedList<String> rst) {
    if(2 == 0 && 2 == 0) {❌
        rst.add(str);
        return;
    }
    if(2 > 0) {
        handle(1, 2, str + "(", rst){ // (
            if(1 == 0 && 2 == 0) {❌
                rst.add(str);
                return;
            }
            if(1 > 0) {
                handle(0, 2, str + "(", rst){ // ((
                    if(0 == 0 && 2 == 0) {❌
                        rst.add(str);
                        return;
                    }
                    if(0 > 0) {
                        ❌
                    }
                    if(2 > 0) {
                        handle(0, 2 - 1, str + ")", rst){ // (()
                            if(left == 0 && right == 0) {❌
                                rst.add(str);
                                return;
                            }
                            if(0 > 0) {
                                ❌
                            }
                            if(right > left) {
                                handle(0, 1 - 1, str + ")", rst){ // (())
                                    if(left == 0 && right == 0) {✅
                                        rst.add(str); // ["(())"]⚡生成一个结果
                                        return;
                                    }
                                    if(left > 0) {
                                        ❌
                                    }
                                    if(right > left) {
                                        ❌
                                    }
                                }
                            }
                        }
                    }
                }
            }
            if(2 > 1) {
                handle(1, 2 - 1, str + ")", rst){ // ()
                    if(left == 0 && right == 0) {
                        ❌
                    }
                    if(left > 0) {
                        handle(1 - 1, 1, str + "(", rst){ // ()(
                            if(left == 0 && right == 0) {
                                rst.add(str);
                                return;
                            }
                            if(left > 0) {
                                ❌
                            }
                            if(right > left) {
                                handle(0, 1 - 1, str + ")", rst) { // ()()
                                    if(left == 0 && right == 0) { ✅
                                        rst.add(str); // ["(())", "()()"]⚡生成一个结果
                                        return;
                                    }
                                    if(left > 0) {
                                        ❌
                                    }
                                    if(right > left) {
                                        ❌
                                    }
                                }
                            }
                        }
                    }
                    if(right > left) {
                        ❌
                    }
                }
            }
        }
    }
    if(2 > 2) {
        ❌
    }
}